Coordinate Confusion

Time to run my 3D autocorrelation function on a mock catalog where we know the answer to try to see if there is a problem with my code or that the reconstruction is failing for another reason. I downloaded the following raw mock LRG catalog from Martin White's web page: halo_000_0.8000.dat.gz. I discovered that I can transfer files to riemann via the insure replacement by doing a two step scp. That is useful to know.

The code I am using to convert from ra, dec (degrees), comoving distance (r) to x, y, z and back:

%  x=r*sin(pi/2-pi/180*dec)*cos(pi/180*ra);
%  y=r*sin(pi/2-pi/180*dec)*sin(pi/180*ra);
%  z=r*cos(pi/2-pi/180*dec) ;

%  r = sqrt(x^2 + y^2 + z^2)
%  dec =  90 - 180/pi*arccos(z/r)
%  ra = 180/pi*arcsin(y/sqrt(x^2 + y^2))

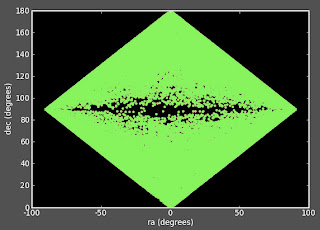
I am a little confused because these mock files are in Cartesian coordinates and if I convert them using the above code into ra and dec, I don't get the objects populating all of ra/dec space:

I constrained the data to be in a sphere of radius 0.5 boxsize (936.0 Mpc/h), and I would think that the ra and dec would then go from 0 to 360 and 0 to 180 respectively.

After some digging, I discovered that by using the arctan2 function I get the proper range:

%  theta = arctan2(sqrt(x^2+y^2), z)
%  phi = arctan2(x, y)

However when I try to then convert back to Cartesian I get a strange answer when I plot the original z versus the converted back z:

This is distressing!

Sources:
http://astro.uchicago.edu/cosmus/tech/code/radecz2xxyyzz.m
http://www.atlasoftheuniverse.com/cosmodis.c
http://www.math.montana.edu/frankw/ccp/multiworld/multipleIVP/spherical/body.htm
http://www.daniweb.com/forums/post860497-2.html

Python tips for the day
1) If you are getting the following error when trying to plot:

RuntimeError: Agg rendering complexity exceeded.
Consider downsampling or decimating your data

Then exit and restart your session and try again and it for some reason works. Stupid python.

2) When converting from spherical use atan2 not asin.